Particle Physics
In the current Standard Model, there are
61
particles that are governed by four fundamental forces.
 In quantum mechanics, wavefunctions for
non-relativistic particles are described by the
Schrödinger equation. In the
relativistic case, three equations, depending on the spin of the particle, are used to describe wavefunctions:
In quantum mechanics, wavefunctions for
non-relativistic particles are described by the
Schrödinger equation. In the
relativistic case, three equations, depending on the spin of the particle, are used to describe wavefunctions:
| Spin |
Equation |
| 0 |
Klein-Gordon Equation |
| 1/2 |
Dirac Equation |
| 1 |
Proca Equation |
The Dirac equation was derived by Pauli Dirac in 1928, and is written:
\[(i\hbar\tilde{\partial}-mc)\psi=0\]
\(\tilde{\partial}\) is the Dirac operator: \(\tilde{\partial}\equiv\gamma^{\mu}\frac{\partial}{\partial x^{\mu}}\). The gamma
matrices are given by:
\[\gamma^0=\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 0 & 0 & -1
\end{bmatrix},\quad\gamma^1=\begin{bmatrix}
0 & 0 & 0 & 1\\
0 & 0 & 1 & 0\\
0 & -1 & 0 & 0\\
-1 & 0 & 0 & 0
\end{bmatrix},\]
\[
\gamma^2=\begin{bmatrix}
0 & 0 & 0 & -i\\
0 & 0 & i & 0\\
0 & i & 0 & 0\\
-i & 0 & 0 & 0
\end{bmatrix},\quad\gamma^3=\begin{bmatrix}
0 & 0 & 1 & 0\\
0 & 0 & 0 & -1\\
-1 & 0 & 0 & 0\\
0 & 1 & 0 & 0
\end{bmatrix}.
\]
\(\gamma^0\) is Hermitian, and the others are anti-Hermitian. All are traceless.
The fifth gamma matrix is defined as:
\[\gamma^5=i\gamma^0\gamma^1\gamma^2\gamma^3=\begin{bmatrix}
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1\\
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0
\end{bmatrix}.\]
\(\gamma^5\) is Hermitian, traceless, and anticommutes with the other gamma matrices: \(\{\gamma^5, \gamma^{\mu}\}=0\).
The Dirac equation has four plane-wave solutions:
\[u^{(1)}=N\begin{bmatrix}
1\\
0\\
\frac{cp_z}{E+mc^2}\\
\frac{c(p_x+ip_y)}{E+mc^2}
\end{bmatrix},\quad u^{(2)}=N\begin{bmatrix}
0\\
1\\
\frac{c(p_x-ip_y)}{E+mc^2}\\
\frac{-cp_z}{E+mc^2}
\end{bmatrix},\]
\[v^{(1)}=N\begin{bmatrix}
\frac{c(p_x-ip_y)}{E+mc^2}\\
\frac{-cp_z}{E+mc^2}\\
0\\
1
\end{bmatrix},\quad v^{(2)}=N\begin{bmatrix}
\frac{cp_z}{E+mc^2}\\
\frac{c(p_x+ip_y)}{E+mc^2}\\
1\\
0
\end{bmatrix}.\]
The normalisation constant is \(N=\sqrt{(E+mc^2)/c}\), from requiring \(u^{\dagger}u=2E/c\). The wavefunction solutions to the
Dirac equation for particles and antiparticles respectively are:
\[Ae^{-ip\cdot x/\hbar}u,\]
\[Ae^{ip\cdot x/\hbar}v.\]
The adjoint Dirac spinors are defined as \(\overline{u}=u^{\dagger}\gamma^0\), and the same for \(\overline{v}\).
Fermi's Golden Rule calculates interaction rates for either collisions or decays. It is given by the product of the kinematic
phase space available for the interaction to occur and the absolute square of the amplitude.
For decays of the form \(1\rightarrow 2+3+\ldots n\), Fermi's Golden Rule is:
\[\Gamma=\frac{S}{2\hbar m_1}\int|\mathscr{M}|^2(2\pi)^4\delta^4(p_1-p_2-p_3-\ldots-p_n)\prod_{i=2}^n\frac{1}{2\sqrt{\underline{p}_i^2+m_i^2c^2}}\frac{\mathrm{d}^3\underline{p}_i}{(2\pi)^3}.\]
This can be simplified for two-body decays of the form \(1\rightarrow 2+3\):
\[\Gamma=\frac{S|\underline{p}|}{8\pi\hbar m_1^2c}|\mathscr{M}|^2,\]
where
\[|\underline{p}|=\frac{c}{2m_1}\sqrt{m_1^4+m_2^4+m_3^4-2m_1^2m_2^2-2m_1^2m_3^2-2m_2^2m_3^2}.\]
In these equations, \(\Gamma\) is the decay rate. Two other quantities of interest, the mean lifetime and the branching ratio,
given respectively below, can be calculated using \(\Gamma\):
\[\tau=\frac{1}{\Gamma},\]
\[\mathcal{B}_i=\frac{\Gamma_i}{\sum_{j}^n\Gamma_j}.\]
For scattering of the type \(1+2\rightarrow 3+4+\ldots n\), Fermi's Golden Rule is:
\[\begin{align}
\sigma=\frac{S\hbar^2}{4\sqrt{(p_1\cdot p_2)^2-(m_1m_2c^2)^2}} & \int|\mathscr{M}|^2(2\pi)^4\delta^4(p_1+p_2-p_3-p_4-\ldots-p_n)\times \\
& \times\prod_{i=3}^n\frac{1}{2\sqrt{\underline{p}_i^2+m_i^2c^2}}\frac{\mathrm{d}^3\underline{p}_i}{(2\pi)^3}.
\end{align}\]
This can be simplified for two-body scattering of the type \(1+2\rightarrow 3+4\):
\[\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}=\left(\frac{\hbar c}{8\pi}\right)^2\frac{S|\mathscr{M}|^2}{(E_1+E_2)^2}\frac{|\underline{p}_f|}{|\underline{p}_i|}.\]
Here, \(|\underline{p}_f|\) is either outgoing momentum, and \(|\underline{p}_i|\) is either incoming momentum. This can then be
integrated over the solid angle \(\mathrm{d}\Omega=|\sin(\theta)\mathrm{d}\theta\mathrm{d}\phi|\) to find the total cross
section, \(\sigma\).
The toy theory is a simplified way of writing scattering amplitudes by using generic
interactions like \(AB\rightarrow AB\) and
\(AA\rightarrow BB\), without specifying the particles or force. The purpose is to serve as a precursor to more complicated
calculations in quantum electrodynamics, quantum chromodynamics, and the
weak force.
The Feynman rules for the toy theory are given below.
Vertices:
For each vertex, write:
\[-ig.\]
Internal Lines:
For internal lines, write:
\[\frac{ig}{q^2-m^2c^2}.\]
Conservation of Momentum:
For each vertex, write:
\[(2\pi)^4\delta^4(k_1\pm k_2\pm k_3),\]
where \({k_i}\) are the four-momenta going into or out of the vertex. If the momentum is going into the vertex, it has a
positive sign, and if it is going out of the vertex, it has a negative sign.
Integration over Internal Momenta:
For each internal line, write an integral over the momentum associated with that line:
\[\frac{1}{(2\pi)^4}\mathrm{d}^4q.\]
Cancel the Delta Function:
The square of the delta function is undefined, so, after integrating, remove the following:
\[\cancel{(2\pi)^4\delta^4(p_1+p_2+\ldots-p_n)}.\]
Lastly, multiply by \(i\).
The completeness relations for fermions and antifermions are:
\[\sum_{s=1,\ 2}u^{(s)}\overline{u}^{(s)}=\tilde{p}+mc,\]
\[\sum_{s=1,\ 2}v^{(s)}\overline{v}^{(s)}=\tilde{p}-mc.\]
The completeness relation for massless particles of spin 1 is:
\[\sum_{s=1,\ 2}\epsilon_i^{(s)}\epsilon_j^{(s)*}=\delta_{ij}-p_ip_j.\]
The completeness relation for massive particles of spin 1 is:
\[\sum_{s=1,\ 2,\ 3}\epsilon_{\mu}^{(s)}\epsilon_{\nu}^{(s)*}=-g_{\mu\nu}+\frac{p_{\mu}p_{\nu}}{M^2c^2}.\]
For experiments in which the spin states of the particles are not specified, the scattering amplitude should be calculated by
averaging over the initial spin states, and summing over the final spin states. Casimir's trick can be used to easily find
matrix elements in scattering amplitudes when summing over spins:
\[\sum_s[\overline{u}(a)\Gamma_1u(b)][\overline{u}(a)\Gamma_2u(b)]^*=\mathrm{Tr}[\Gamma_1(\tilde{p}_b+m_bc)\overline{\Gamma}_2(\tilde{p}_a+m_ac)].\]
If \(v\) is used instead of \(u\), the sign of the mass becomes negative. In this equation, \(\tilde{p}\) is the Dirac operator:
\[\tilde{p}\equiv\gamma^{\mu}p_{\mu}=\begin{bmatrix}
E & -\sigma\cdot\underline{p}\\
\sigma\cdot\underline{p} & -E
\end{bmatrix},\]
where the dot product is:
\[\sigma\cdot\underline{p}=\sigma_x p_x+\sigma_y p_y+\sigma_z p_z=\begin{bmatrix}
p_z & p_x-ip_y\\
p_x+ip_y & -p_z
\end{bmatrix}.\]
Quantum electrodynamics (QED) describes the electromagnetic force, through which the photon couples to particles with electric
charge (everything but neutrinos). It is described by the \(U(1)\) symmetry group, and the three \(2\times 2\) traceless
Hermitian Pauli spin matrices:
\[\sigma_x=\begin{bmatrix}
0 & 1\\
1 & 0
\end{bmatrix},\quad\sigma_y=\begin{bmatrix}
0 & -i\\
i & 0
\end{bmatrix},\quad\sigma_z=\begin{bmatrix}
1 & 0\\
0 & -1
\end{bmatrix}.\]
The Feynman rules for QED are given below. "Electron" refers to any charged fermion, and "positron" refers to any charged
antifermion.
External Lines:
| Particle |
Wavefunction |
| Incoming Electron |
\(u\) |
| Outgoing Electron |
\(\overline{u}\) |
| Incoming Positron |
\(\overline{v}\) |
| Outgoing Positron |
\(v\) |
| Incoming Photon |
\(\epsilon_{\mu}\) |
| Outgoing Photon |
\(\epsilon_{\mu}^*\) |
Vertices:
For each vertex, write:
\[ig_e\gamma^{\mu}.\]
Internal Lines:
For internal photon lines, write:
\[\frac{-ig_{\mu\nu}}{q^2}.\]
For internal electron or positron lines, write:
\[\frac{i(\gamma^{\mu}q_{\mu}+mc)}{q^2-m^2c^2}.\]
After this, for conservation of energy and momentum, for each vertex, write \((2\pi)^4\delta^4(k_1\pm k_2\pm k_3)\), where the
sign is positive for momenta going into the vertex, and is negative for those going out. Then, for each internal line, write
\((2\pi)^{-4}\mathrm{d}^4q\) and integrate. Finally, multiply by \(i\) and cancel the delta function by writing
\((2\pi)^4\delta^4(p_1+p_2+\ldots-p_n)\).
Quantum chromodynamics (QCD) describes the strong force, through which 8 gluons couple to particles with colour charge (quarks
and gluons). It is described by the \(SU(3)\) symmetry group, which has 8 traceless \(3\times 3\) generator matrices, describing
the 8 gluons:
\[\lambda^1=\begin{bmatrix}
0 & 1 & 0\\
1 & 0 & 0\\
0 & 0 & 0
\end{bmatrix},\quad\lambda^2=\begin{bmatrix}
0 & -i & 0\\
i & 0 & 0\\
0 & 0 & 0
\end{bmatrix},\quad\lambda^3=\begin{bmatrix}
1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & 0
\end{bmatrix},\quad\lambda^4=\begin{bmatrix}
0 & 0 & 1\\
0 & 0 & 0\\
1 & 0 & 0
\end{bmatrix},\]
\[\lambda^5=\begin{bmatrix}
0 & 0 & -i\\
0 & 0 & 0\\
i & 0 & 0
\end{bmatrix},\quad\lambda^6=\begin{bmatrix}
0 & 0 & 0\\
0 & 0 & 1\\
0 & 1 & 0
\end{bmatrix},\quad\lambda^7=\begin{bmatrix}
0 & 0 & 0\\
0 & 0 & -i\\
0 & i & 0
\end{bmatrix},\quad\lambda^8=\frac{1}{\sqrt{3}}\begin{bmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & -2
\end{bmatrix}.\]
The commutator of two lambda matrices gives the corresponding \(SU(3)\) structure constant:
\[[\lambda^{\alpha}, \lambda^{\beta}]=2if^{\alpha\beta\gamma}\lambda^{\gamma}\]
Summation over \(\gamma\) goes from 1 to 8. This relation implies that all \(\lambda\) matrices are tracless, which can be
verified by looking at the matrices above.
The Feynman rules for QCD are given below.
External Lines:
| Particle |
Wavefunction |
| Incoming Quark |
\(uc\) |
| Outgoing Quark |
\(\overline{u}c^{\dagger}\) |
| Incoming Antiquark |
\(\overline{v}c^{\dagger}\) |
| Outgoing Antiquark |
\(vc\) |
| Incoming Gluon |
\(\epsilon_{\mu}a^{\alpha}\) |
| Outgoing Gluon |
\(\epsilon_{\mu}^*a^{\alpha *}\) |
Vertices:
For a quark-gluon vertex, write:
\[\frac{ig_s}{2}\lambda^{\alpha}\gamma^{\mu}.\]
For a three-gluon vertex, write:
\[-g_sf^{\alpha\beta\gamma}[g_{\mu\nu}(k_2-k_3)_{\lambda}+g_{\nu\lambda}(k_2-k_3)_{\mu}+g_{\lambda\mu}(k_3-k_1)_{\nu}].\]
For a four-gluon vertex, write:
\[-ig_s^2[f^{\alpha\beta\eta}f^{\gamma\delta\eta}(g_{\mu\lambda}g_{\nu\rho}-g_{\mu\rho}g_{\nu\lambda})+f^{\alpha\delta\eta}f^{\beta\gamma\eta}(g_{\mu\nu}g_{\lambda\rho}-g_{\mu\lambda}g_{\nu\rho})+f^{\alpha\gamma\eta}f^{\delta\beta\eta}(g_{\mu\rho}g_{\nu\lambda}-g_{\mu\nu}g_{\lambda\rho})].\]
Internal Lines:
For internal gluon lines, write:
\[\frac{-ig_{\mu\nu}\delta^{\alpha\beta}}{q^2}.\]
For internal quark or antiquark lines, write:
\[\frac{i(\tilde{q}+mc)}{q^2-m^2c^2}.\]
\(\tilde{q}\) is the Dirac operator \(\tilde{q}\equiv\gamma^{\mu}q_{\mu}\).
Colour Factors
?
The weak force is mediated by massive \(W^{\pm}\) and \(Z^0\) bosons, which couple to all leptons. They are they only
force-mediating particles that couple to neutrinos. It is described by the \(SU(2)\) symmetry group, which has the three
\(2\times 2\) Pauli spin matrices as generators.
The Feynman rules for the weak force are given below.
External Lines:
| Particle |
Wavefunction |
| Incoming Particle |
\(u\) |
| Outgoing Particle |
\(\overline{u}\) |
| Incoming Antiparticle |
\(\overline{v}\) |
| Outgoing Antiparticle |
\(v\) |
| Incoming Boson |
\(\epsilon_{\mu}\) |
| Outgoing Boson |
\(\epsilon_{\mu}^*\) |
Vertices:
For an interaction proceeding via a \(W^{\pm}\) boson, write:
\[\frac{-ig_w}{2\sqrt{2}}\gamma^{\mu}(1-\gamma^5).\]
For an interaction proceeding via a \(Z^0\) boson, write:
\[\frac{-ig_z}{2}\gamma^{\mu}\left(c_V^f-c_A^f\gamma^5\right).\]
Internal Lines:
For internal lines (\(W^{\pm}\) or \(Z^0\)), write:
\[\frac{-i(g_{\mu\nu}-(q_{\mu}q_{\nu}/M^2c^2))}{q^2-M^2c^2},\]
where \(M\) is either \(M_Z\) or \(M_W\).
If \(q^2\ll M^2c^2\), write:
\[\frac{ig_{\mu\nu}}{M^2c^2}.\]
The vector and axial vector couplings are different for each type of fermion:
| Fermion |
\(c_V\) |
\(c_A\) |
| \(\nu_e,\ \nu_{\mu},\ \nu_{\tau}\) |
0.5 |
0.5 |
| \(e,\ \mu,\ \tau\) |
-0.0372 |
-0.5 |
| \(u,\ c,\ t\) |
0.19147 |
0.5 |
| \(d,\ s,\ b\) |
-0.34573 |
-0.5 |
Isospin - Ratio of Cross Sections
Find the ratio of cross sections for the two interactions of \(\pi^-+p\) and the interaction of \(\pi^++p\). Assume the
\(I=3/2\) channel dominates.
The three interactions are:
\[\pi^-+p\rightarrow K^0+\Sigma^0,\]
\[\pi^-+p\rightarrow K^++\Sigma^-,\]
\[\pi^++p\rightarrow K^++\Sigma^0.\]
Label them A, B, and C respectively. The isospins of the particles are given in the form \(\ket{I,\ I_3}\) as:
| Particle |
Isospin |
Particle |
Isospin |
| \(\pi^-\) |
\(\ket{1,\ -1}\) |
\(K^+\) |
\(\ket{1/2,\ 1/2}\) |
| \(\pi^+\) |
\(\ket{1,\ 1}\) |
\(\Sigma^-\) |
\(\ket{1,\ -1}\) |
| \(p\) |
\(\ket{1/2,\ 1/2}\) |
\(\Sigma^0\) |
\(\ket{1,\ 0}\) |
| \(K^0\) |
\(\ket{1/2,\ -1/2}\) |
\(\Sigma^+\) |
\(\ket{1,\ 1}\) |
For interaction A, the left-hand side is given by the product of the isospins of \(\pi^-\) and \(p\), which should then be
decomposed using a
Clebsch-Gordan table:
\[\ket{1,\ -1}\ket{1/2,\ 1/2}=\sqrt{\frac{1}{3}}\ket{3/2,\ -1/2}-\sqrt{\frac{2}{3}}\ket{1/2, -1/2}.\]
The same should be done to the right-hand side, using the isospins of \(K^0\) and \(\Sigma^0\):
\[\ket{1/2,\ -1/2}\ket{1,\ 0}=\sqrt{\frac{2}{3}}\ket{3/2,\ -1/2}+\sqrt{\frac{1}{3}}\ket{1/2, -1/2}.\]
Both contain the same kets in the decompositions, and therefore both will contribute to the amplitude \(\mathscr{M}_A\).
Let the amplitude associated with \(I=3/2\) be \(\mathscr{M}_3\), and with \(I=1/2\) be \(\mathscr{M}_1\). Then:
\[\begin{align}
\mathscr{M}_A & =\sqrt{\frac{1}{3}}\sqrt{\frac{2}{3}}\mathscr{M}_3+\left(-\sqrt{\frac{2}{3}}\right)\sqrt{\frac{1}{3}}\mathscr{M}_1,\\
& =\frac{\sqrt{2}}{3}\left(\mathscr{M}_3-\mathscr{M}_1\right)
\end{align}\]
The same can be done for interactions B and C to give, respectively:
\[\mathscr{M}_B=\frac{1}{3}\left(2\mathscr{M}_1-\mathscr{M}_3\right),\]
\[\mathscr{M}_C=\mathscr{M}_3.\]
The cross section is proportional to the absolute square of the amplitude. The ratio of cross sections will be:
\[\begin{align}
\sigma_A:\sigma_B:\sigma_C & =\mathscr{M}_A^2:\mathscr{M}_B^2:\mathscr{M}_C^2,\\
& =\frac{2}{9}\left(\mathscr{M}_3-\mathscr{M}_1\right)^2:\frac{1}{9}\left(2\mathscr{M}_1+\mathscr{M}_3\right)^2:\mathscr{M}_3^2,\\
& =2\left(\mathscr{M}_3-\mathscr{M}_1\right)^2:\left(2\mathscr{M}_1+\mathscr{M}_3\right)^2:9\mathscr{M}_3^2.
\end{align}\]
Assuming the \(I=3/2\) channel dominates, let \(\mathscr{M}_1\) be negligible, and divide through by the common factor of
\(\mathscr{M}_3^2\). The ratio of cross sections is therefore:
\[\boxed{\sigma_A:\sigma_B:\sigma_C=2:1:9}.\]
Toy Theory - Differential Cross Section in the Center of Mass Frame
Find the differential cross section (at tree-level) for the interaction \(A+B\rightarrow A+B\) in the center of mass frame.
Assume the particle masses of particles A and B are the same, and that the mass of particle C is 0. Express the result in terms
of the initial energy and the scattering angle of particle A.
From the
Mandelstam variables, the interaction
can proceed via the \(s\)-channel and the \(t\)-channel. Starting with the \(s\)-channel, using the toy theory Feynman rules,
the pieces of the diagram can be written:
| Piece |
Factor |
| First Vertex |
\(-ig\) |
| Propagator |
\(i/(q^2-m_C^2c^2)\) |
| Second Vertex |
\(-ig\) |
| First Conservation |
\((2\pi)^4\delta^4(p_1-p_4-q)\) |
| Second Conservation |
\((2\pi)^4\delta^4(q+p_2-p_3)\) |
| Internal Integral |
\((1/2\pi)^4\mathrm{d}q^4\) |
Combining these gives the \(s\)-channel amplitude:
\[\mathscr{M}_s=\int(-ig)^2\left(\frac{i}{q^2-m_C^2c^2}\right)(2\pi)^4\delta^4(p_1-p_4-q)(2\pi)^4\delta^4(q+p_2-p_3)\frac{\mathrm{d}^4q}{(2\pi)^4}.\]
After simplifying, performing the integral, and then cancelling the final delta function, this becomes:
\[\mathscr{M}_s=\frac{g^2}{(p_1-p_4)^2-m_C^2c^2}.\]
The mass can be set to 0, and the momentum relation is simply \(sc^2\). The convenience of the Mandelstam variables is that the
\(t\)-channel amplitude can now immediately be written, without doing the calculation. Therefore:
\[\mathscr{M}_s=\frac{g^2}{sc^2},\quad\mathscr{M}_t=\frac{g^2}{tc^2}.\]
The total amplitude will be the sum of both:
\[\mathscr{M}=\mathscr{M}_s+\mathscr{M}_t=g^2\left(\frac{1}{(p_1-p_4)^2}+\frac{1}{(p_1+p_2)^2}\right).\]
This can now be inserted into
Fermi's Golden Rule for scattering to find the differential
cross section:
\[\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}=\left(\frac{\hbar c}{8\pi}\right)^2\frac{S|\mathscr{M}|^2}{(E_1+E_2)^2}\frac{|\underline{p}_4|}{|\underline{p}_1|},\]
where \(S=1\). First, write the four-momentum of each particle. Because the problem is being analysed in the center of mass
frame, the momenta of particles A and B will be equal and opposite. Because the masses are equal, they will have equal energies
as well, and will be called \(E\). Therefore:
\[p_1=\left[\frac{E}{c},\ \underline{p}_1\right],\quad p_2=\left[\frac{E}{c},\ -\underline{p}_1\right],\]
\[p_3=\left[\frac{E}{c},\ \underline{p}_3\right],\quad p_4=\left[\frac{E}{c},\ -\underline{p}_3\right].\]
These imply \(|\underline{p}_4|=|\underline{p}_1|\), and the differential cross section can be simplified:
\[\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}=\left(\frac{\hbar c}{8\pi}\right)^2\frac{|\mathscr{M}|^2}{4E^2}.\]
The momenta can be used inside the amplitude to express this in terms of the scattering angle. First, for the
\(\mathscr{M}_s\) part:
\[p_1-p_4=[0,\ \underline{p}_1+\underline{p}_3],\]
\[\begin{align}
(p_1-p_4)^2 & =0-(\underline{p}_1+\underline{p}_3)^2,\\
& =-(\underline{p}_1^2+\underline{p}_3^2+2\underline{p}_1\cdot\underline{p}_3),\\
& =-2\underline{p}_1^2-2|\underline{p}_1||\underline{p}_3|\cos(\theta),\\
& =-4\underline{p}_1^2\cos^2(\theta/2).
\end{align}\]
The fourth line was calculated by using \(|\underline{p}_1|=|\underline{p}_3|\), as above, as well as the trigonometric
half-angle identity \(2\cos^2(\theta/2)=1+\cos(\theta)\).
Now for the \(\mathscr{M}_t\) part:
\[p_1+p_2=\left[\frac{2E}{c},\ \underline{0}\right],\]
\[(p_1+p_2)^2=\frac{4E^2}{c^2}.\]
The absolute square of the amplitude is then:
\[\begin{align}
|\mathscr{M}|^2 & =g^4\left(\frac{-1}{4\underline{p}_1^2\cos^2(\theta/2)}+\frac{c^2}{4E^2}\right)^2,\\
& =\frac{g^4}{16}\left(\frac{c^2}{E^2}-\frac{1}{\underline{p}_1^2\cos^2(\theta/2)}\right)^2.
\end{align}\]
From the
energy-mass relation,
\(\underline{p}_1^2\) can be replaced:
\[\begin{align}
|\mathscr{M}|^2 & =\frac{g^4}{16}\left(\frac{c^2}{E^2}-\frac{1}{(E^2-m^2c^4)\cos^2(\theta/2)}\right)^2,\\
& =\frac{g^4}{16}\left(\frac{(E^2\tan^2(\theta/2)+m^2c^4)c^2}{E^2(E^2-m^2c^4)}\right)^2.
\end{align}\]
Substitute this into the differential cross section:
\[\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}=\left(\frac{\hbar c}{8\pi}\right)^2\left(\frac{1}{2E}\right)^2\left(\frac{g^2}{4}\frac{(E^2\tan^2(\theta/2)+m^2c^4)c^2}{E^2(E^2-m^2c^4)}\right)^2.\]
Grouping terms inside the squares gives the differential cross section as:
\[\boxed{\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}=\left(\frac{\hbar c^3g^2}{64\pi}\cdot\frac{E^2\tan^2(\theta/2)+m^2c^4}{E^3(E^2-m^2c^4)}\right)^2}.\]
QCD - Quark-Antiquark Colour Factor
Calculate the colour factor for a quark annihilating with an antiquark into a gluon then producing a new quark-antiquark
pair, assuming the quarks are in a colour octet state.
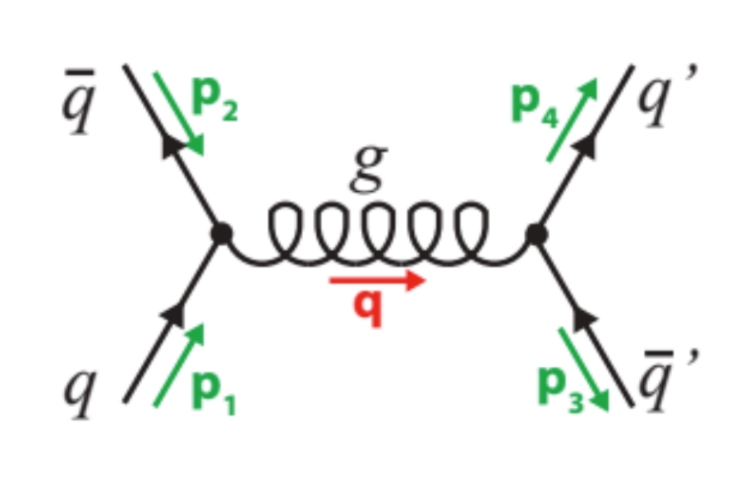
Using the
QCD Feynman rules, the pieces of the diagram can be written:
| Piece |
Factor |
| Incoming Antiquark |
\(\overline{v}(2)c_2^{\dagger}\) |
| Quark-Gluon Vertex |
\((-ig_s/2)\lambda^{\alpha}\gamma^{\mu}\) |
| Incoming Quark |
\(u(1)c_1\) |
| Internal Gluon |
\(-ig_{\mu\nu}\delta^{\alpha\beta}/q^2\) |
| Outgoing Quark |
\(\overline{u}(3)c_3^{\dagger}\) |
| Quark-Gluon Vertex |
\((-ig_s/2)\lambda^{\beta}\gamma^{\nu}\) |
| Outgoing Antiquark |
\(v(4)c_4\) |
The amplitude is then:
\[\mathscr{M}=i[\overline{v}(2)c_2^{\dagger}\left(\frac{-ig_s}{2}\right)(\lambda^{\alpha}\gamma^{\mu})u(1)c_1]\left(\frac{-ig_{\mu\nu}\delta^{\alpha\beta}}{q^2}\right)[\overline{u}(3)c_3^{\dagger}\left(\frac{-ig_s}{2}\right)(\lambda^{\beta}\gamma^{\nu})v(4)c_4].\]
After cancelling all the factors of \(i\) and rearranging, this is:
\[\mathscr{M}=-\left(\frac{g_s^2}{4q^2}\right)[\overline{v}(2)\gamma^{\mu}u(1)][\overline{u}(3)\gamma_{\mu}v(4)](c_2^{\dagger}\lambda^{\alpha}c_1)(c_3^{\dagger}\lambda^{\alpha}c_4).\]
Compared to the same interaction proceeding via exchange of a photon instead of a gluon, this amplitude is different by a
factor of \(f\), the colour factor (as well as containing \(g_s\) instead of \(g_e\)):
\[f=\frac{1}{4}(c_2^{\dagger}\lambda^{\alpha}c_1)(c_3^{\dagger}\lambda^{\alpha}c_4).\]
Without loss of generality (due to colour symmetry), let \(c_1\) be red and \(c_2\) be blue. Then \(c_3\) is blue, and
\(c_4\) is red. The colour factor can then be evaluated using the colour state corresponding to \(r\) and \(b\):
\[f=\frac{1}{4}\left(\begin{bmatrix}
0 & 1 & 0
\end{bmatrix}\lambda^{\alpha}\begin{bmatrix}
1\\
0\\
0
\end{bmatrix}\right)\left(\begin{bmatrix}
1 & 0 & 0
\end{bmatrix}\lambda^{\alpha}\begin{bmatrix}
0\\
1\\
0
\end{bmatrix}\right)=\frac{1}{4}\lambda^{\alpha}_{21}\lambda^{\alpha}_{12}.\]
Summation over \(\alpha\) is implied by the repeated index. Looking at the
lambda matrices, \(\lambda^1\) and
\(\lambda^2\) have entries in the \(21\) and \(12\) positions. Therefore:
\[\begin{align}
f & =\frac{1}{4}(\lambda^1_{21}\lambda^1_{12}+\lambda^2_{21}\lambda^2_{12}),\\
& =\frac{1}{4}((1)(1)+(i)(-i)).
\end{align}\]
Therefore, the colour factor is:
\[\boxed{f=\frac{1}{2}}.\]
Weak Force - Branching Ratio for Z Boson Decay
Calculate the branching ratio for the decay of a \(Z^0\) boson into an electron and positron.
The first step is to calculate the total decay rate for \(Z^0\) decay. The \(Z^0\) boson can decay into any fermion-antifermion
pair. Using the
weak force Feynman rules, the pieces of the diagram can be written:
| Piece |
Factor |
| Incoming \(Z^0\) Boson |
\(\epsilon_{\mu}(1)\) |
| \(Z^0\) Vertex |
\((-ig_Z/2)\gamma^{\mu}(c_V^f-c_A^f\gamma^5)\) |
| Outgoing Fermion |
\(\overline{u}(2)\) |
| Outgoing Antifermion |
\(v(3)\) |
The amplitude is then:
\[\begin{align}
\mathscr{M} & =\epsilon_{\mu}(1)\overline{u}(2)\left(\frac{-ig_Z}{2}\right)\gamma^{\mu}(c_V^f-c_A^f\gamma^5)v(3),\\
& =\left(\frac{-ig_Z}{2}\right)\epsilon_{\mu}(1)\overline{u}(2)\Gamma_fv(3),
\end{align}\]
where \(\Gamma_f=\gamma^{\mu}(c_V^f-c_A^f\gamma^5)\). This can now be inserted into
Fermi's Golden Rule
for decays to find the decay rate:
\[\Gamma=\frac{S|\underline{p}|}{8\pi\hbar m_1^2c}|\mathscr{M}|^2.\]
This requires squaring the amplitude:
\[\begin{align}
|\mathscr{M}|^2 & =\left(\frac{g_Z^2}{4}\right)\epsilon_{\mu}(1)\epsilon_{\nu}^*(1)[\overline{u}(2)\Gamma_fv(3)][\overline{u}(2)\Gamma_fv(3)]^*,\\
& =\left(\frac{g_Z^2}{4}\right)\epsilon_{\mu}(1)\epsilon_{\nu}^*(1)[\overline{u}(2)\Gamma_fv(3)][\overline{v}(3)\overline{\Gamma}_fu(2)].
\end{align}\]
The conjugate transpose of the \(\Gamma_f\) operator must be found:
\[\begin{align}
\overline{\Gamma}_f & =\gamma^0\Gamma_f^{\dagger}\gamma^0,\\
& =\gamma^0(\gamma^{\nu}(c_V^f-c_A^f\gamma^5))^{\dagger}\gamma^0,\\
& =\gamma^0(c_V^f-c_A^f\gamma^5)^{\dagger}(\gamma^{\nu})^{\dagger}\gamma^0,\\
& =\gamma^0(c_V^{f*}-c_A^{f*}(\gamma^5)^{\dagger})(\gamma^{\nu})^{\dagger}\gamma^0,\\
& =(c_V^{f}-c_A^{f}\gamma^5)\gamma^0(\gamma^{\nu})^{\dagger}\gamma^0,\\
& =(c_V^{f}-c_A^{f}\gamma^5)\gamma^{\nu}.
\end{align}\]
In the fifth line,
the property that \(\gamma^5\) is Hermitian was used, as well as the
the property that the vector and axial vector couplings are real for all fermions.
The absolute square of the amplitude is now:
\[|\mathscr{M}|^2=\left(\frac{g_Z^2}{4}\right)\epsilon_{\mu}(1)\epsilon_{\nu}^*(1)[\overline{u}(2)\gamma^{\mu}(c_V^f-c_A^f\gamma^5)v(3)][\overline{v}(3)(c_V^{f*}-c_A^{f*}\gamma^5)\gamma^{\nu}u(2)].\]
Use
Casimir's trick to sum over the spins of the fermions:
\[\begin{align}
|\mathscr{M}|^2 & =\left(\frac{g_Z^2}{4}\right)\epsilon_{\mu}(1)\epsilon_{\nu}^*(1)\mathrm{Tr}[\Gamma_f(\tilde{p}_3-m_3c)\overline{\Gamma}_f(\tilde{p_2}-m_2c)],\\
& =\left(\frac{g_Z^2}{4}\right)\epsilon_{\mu}(1)\epsilon_{\nu}^*(1)\mathrm{Tr}[\Gamma_f\tilde{p}_3\overline{\Gamma}_f\tilde{p_2}],\\
& =\left(\frac{g_Z^2}{4}\right)\epsilon_{\mu}(1)\epsilon_{\nu}^*(1)\mathrm{Tr}[\gamma^{\mu}(c_V^f-c_A^f\gamma^5)\gamma^{\lambda}p_{3\lambda}(c_V^{f}-c_A^{f}\gamma^5)\gamma^{\nu}\gamma^{\sigma}p_{2\sigma}].
\end{align}\]
where \(\tilde{p}_i\) is the Dirac operator \(\tilde{p}_i\equiv\gamma^{\mu}p_{i\mu}\). The masses of the fermions were assumed
to be negligible.
The
completeness relation can be used to sum over the spins of the \(Z^0\) boson:
\[|\mathscr{M}|^2=\left(\frac{g_Z^2}{4}\right)\left(-g_{\mu\nu}+\frac{p_{1\mu}p_{2\nu}}{M_Zc^2}\right)\mathrm{Tr}[\Gamma_f\tilde{p}_3\overline{\Gamma}_f\tilde{p_2}].\]


